אלגוריתם חדש ומדויק לאיסוף מידע

This post is also available in: English (אנגלית)

כשאי אפשר לאסוף את כל המידע הדרוש, אלגוריתם חדש יכול לסייע לנו להתמקד בנתונים מסויימים בלבד. טכניקה חדשה זו יכולה לסייע באיסוף המידע הנכון ולקצר את משך התהליך כולו.

חלק נכבד מחקר הבינה המלאכותית עוסק באתגר ביצוע ניבויים על סמך כמויות גדולות של נתונים. דוגמה בולטת אחת, כך לפי MIT News, היא מנועי ההמלצות באתרי קניות כמו אמזון ונטפליקס.

כמה סוגים של נתונים, עם זאת, בעייתיים יותר לאיסוף לעומת מספר הלחיצות באתרי קניות – מידע על תצורות גיאולוגיות בעומק של קילומטרים מתחת לפני השטח, למשל. כשמדובר ביישומים אחרים – כמו ניסיון לנבא את מסלולה של סופה – לפעמים אין מספיק זמן כדי לעבד את כל המידע הזמין.

דן לוין, סטודנט בבית הספר לאווירונאוטיקה וחלל ב-MIT, ביחד עם היועץ שלו ג'ונת'ן האו, פיתחו טכניקה חדשה שעשוייה לעזור בפתרון שתי הבעיות. בתחומים שבהם איסוף המידע הוא קשה במיוחד – או דורש זמן עיבוד ארוך במיוחד – הטכניקה יכולה לסייע באיתור קבוצות הנתונים המסויימות שבעזרתן ניתן להגיע לתוצאות האמינות ביותר. גיאולוגים שמנסים להעריך את היקפם של מאגרי נפט, או מטאורולוגים שמנסים לחזות את מזג האוויר, יכולים להסתפק במספר מצומצם של מדידות מדוייקות במיוחד וכך לחסוך זמן וכסף.

לוין והאו מביטים על מקרה מיוחד שבו אנו יודעים מראש משהו על היחס שבין נתונים שונים. חיזוי מזג אוויר הוא דוגמה אינטואיטיבית: מדידות טמפרטורה, לחץ אוויר ומהירות רוח במקום אחד יהיו ככל הנראה דומות למדידות במקומות סמוכים, או למדידות באותו מקום זמן קצר לאחר מכן – אבל ההתאמה הולכת ונחלשת ככל שמתרחקים בזמן או במרחב.

iHLS – Israel Homeland Security

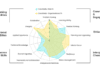
התאמות מהסוג הזה אפשר לייצג על ידי מה שמכונה "מודל גרפי הסתברותי" (probabilistic graphical model). בהקשר הזה גרף הוא ייצוג מתמטי שמורכב ממרכזים (nodes) – בדרך כלל מיוצגים על ידי מעגלים – ומקצוות (edges) – שמתוארים כפסים המקשרים בין המרכזים. תרשים רשת הוא דוגמה אחת של גרף, עץ משפחה הוא דוגמה נוספת. במודל הגרפי ההסתברותי המרכזים מייצגים משתנים, והקצוות מייצגים את העוצמה של היחסים ביניהם.

לוין והאו פיתחו אלגוריתם שיכול לחשב ביעילות כמה מידע אפשר להפיק מכל מרכז בגרף על כל מרכז אחר – מה שידוע בתורת המידע כ"מידע הדדי" (mutual information). לדברי לוין, אחד מהמכשולים שמפריעים ליעילות החישוב היא נוכחות של "לולאות" בגרף, או מרכזים שמחוברים אחד לשני בכמה דרכים.

חישוב מידע הדדי בין מרכזים, אומר לוין, דומה להזרקת צבע כחול אל תוך אחד מהם ומדידות ריכוז הצבע הכחול במרכזים אחרים. “בדרך כלל הריכוז יורד ככל שמתרחקים אל תוך הגרף", אמר לוין. “אם יש מסלול ייחודי שמקשר ביניהם אנחנו יכולים לחשב אותו בקלות יחסית, בגלל שאנחנו יודעים באיזה מסלול עובר הצבע הכחול. לעומת זאת, אם יש לולאות בגרף, קשה לנו יותר לחשוב עד כמה יכחילו המרכזים האחרים, כי הצבע יכול לעבור ביניהם בכמה דרכים.”

השלב הראשון בטכניקה של החוקרים, אם כך, הוא להתגבר על הבעיה הזאת. הדבר נעשה על ידי חישוב מתמטי שיוצר "עצי גישור" (spanning trees) עבור הגרף. “עץ" מתמטי מהסוג הזה הוא גרף ללא לולאות. בעץ משפחתי, למשל, לולאה משמעותה שאדם הוא גם האבא וגם האח של אדם אחר. עץ גישור הוא עץ שנוגע בכל המרכזים שבגרף, אבל נמנע מהקצוות שיוצרים לולאות.